What Is Swarm Problem Solving?
contributed by Dr. Jamie Schwandt, (Ed.D.)
“It would be unlikely that it would be a fish that discovered water, or a bird air.” – Chinese Proverb
A common metaphor used by Arthur Conan Doyle in his Sherlock Holmes stories is that of links, chains, and threads. Alan Macfarlane writes in On Creative And Analytical Methods, that links, chains, and threads are metaphors in which Holmes often uses to explain how he moves backward through a set of problems or causes. Macfarlane explains that he uses a series of threads leading him through the maze of facts.
Macfarlane discusses the importance of being able to reason backward, where one starts at the end of the chain and works backward to the causes. In Doyle’s A Study in Scarlet, the character Sherlock Holmes explains,
“Most people, if you describe a train of events to them, will tell you what the result would be. They can put those events together in their minds, and argue from them that something will come to pass. There are a few people, however, who, if you told them a result, would be able to evolve from their own inner consciousness what the steps were which led up to that result. This power is what I mean which I talk of reasoning backwards, of analytically.”
Doyle’s writing and the metaphor of links, chains, and threads inspired the creation of this problem-sensing and problem-solving methodology. Furthermore, Swarm Problem Sensing and Solving should be considered as Swarm Questions – Type II. For which this will serve as a deeper form of questioning when compared to my writing on Swarm Questions: What Have? What Should? What If? – which should be considered as Swarm Questions – Type I.
Moreover, problems are often complex and confusing. We must make sure we are solving the right problem. As William N. Dunn writes in Public Policy Analysis ed. 5, we typically do not begin with clearly articulated problems, but with a sense of diffuse worries and inchoate signs of stress. Thus, we must first sense the correct problem before we attempt to structure and solve a problem.
Abductive Logic – How Best Explanations Can Be Overturned
“What comes before the model is an intuition of what rules for the patterns could be. I put that together into a skeleton, and then I add in a lot of detail about how the termites and the plants actually function. It’s like detective work.”— Corina Tarnita, quoted in Underbug: An Obsessive Tale of Termites and Technology
Swarm Problem-Sensing and Solving uses abductive reasoning. In The Making of an Expert Detective. Thinking and Deciding in Criminal Investigations, Ivar Fahsing remarked, “Abductive logic is widely recognized as a powerful mechanism for hypothetical reasoning in the absence of complete knowledge and is generally understood as reasoning from effects to causes.” Fahsing posits, “Abduction has been described as ‘the logic of what might be’ and unlike deduction, but similar to induction, the conclusions from an abductive argument might turn out to be false, even if the premises are true. Unlike induction, abductive logic allows for qualified and pragmatic guessing.”
There are significant distinctions between the three categories of logic or reasoning: deductive, inductive, and abductive reasoning. Fahsing provides an explanation and example for each. Let’s take a quick look:
Deductive Reasoning
Explanation: In deductive reasoning, the conclusion is a direct result of the facts presented.
Example: Tim cannot see (fact). The condition when you cannot see is known as blindness (fact). Hence, Tim is blind (deduction).
Inductive Reasoning
Explanation: In inductive reasoning, the conclusion is derived from a fact, but an inference is added.
Example: Tim cannot see (fact). All people who cannot see have probably bumped into many objects compared to people who can see (inference). Tim will have more accidents than people who can see (induction).
Abductive Reasoning
Explanation: In abductive reasoning, we try to presume potential facts by using supporting facts.
Example: Some people cannot see (fact). Tim continued walking into objects (supporting fact). Tim might possibly be blind (abduction).
Abductive reasoning is a synthesis of inductive and deductive reasoning and allows an individual to pose a simple question that cannot be asked in the other forms of reasoning: “What could be so?” Fahsing provides one last example demonstrating the utility of abductive reasoning. He uses an example from Arthur Conan Doyle’s “The Silver Blaze”. He posits, in abductive logic, there is often no room for true falsification. In “The Silver Blaze,” Sherlock Holmes and Scotland Yard Detective Inspector Gregory are discussing the theft of a racehorse from a country estate that is guarded by a fierce watchdog:
Gregory: “You consider that to be important?”
Holmes: “Exceedingly so.”
Gregory: “Is there any point to which you would wish to draw my attention?”
Holmes: “To the curious incident of the dog in the night-time.”
Gregory: “The dog did nothing in the night-time.”
Holmes: “That was the curious incident.”
In the story, Holmes explains how the “dog that didn’t bark” helped him solve the crime. Holmes remarked, “I had grasped the significance of the silence of the dog, for one true inference invariably suggests others… A dog was kept in the stables, and yet, though someone had been in, and had fetched out a horse, he had not barked enough to arouse the two lads in the loft. Obviously, the midnight visitor was someone whom the dog knew well.”
Fahsing explains that Holmes makes an inference from known facts to explain them: Holmes is working on the premise that because (a) dogs bark loudly at strangers, but not at people they know; and (b) the dog didn’t bark loudly, if he barked at all; then (c) the dog knew the intruder.
Fahsing concludes,
“That sounds fine at first. This is perhaps how many detectives resolve an investigative challenge, but this seemingly strong piece of deductive reasoning is in reality based on weak or absent information and therefore it is abductive and non-monotonic. Holmes assumes that the watchdog behaves in a particular manner when, in fact, there might be various reasons why the dog wouldn’t bark. Firstly, the dog might have barked, but no one heard. Secondly, the stranger might have brought a sausage to appease the dog. A third possibility is the dog had been drugged. Because Holmes did not take these variables into consideration, one might conduce that the logic of Holmes’s argument is weak and not necessarily the best explanation. A true detective should know that this is a hypothesis based on probability that dogs normally bark at strangers – not an absolute fact. Hence, several competing explanations may be true and even the best explanation can be overturned by new diagnostic information.”
Scaffolding Curiosity
“Curiosity overwhelms insecurity, and renders irrelevant any risk of overconfidence. With the necessary skills to scaffold this curiosity, design action – making things – is transformed into an environment of deep inquiry.”— Ann M. Pendleton-Jullian and John Seely Brown, quoted in Design Unbound: Designing For Emergence In A White Water World
The following mental models and techniques, along with Doyle’s writing, were used to develop this idea.
Fuzzy Trace Theory: Professor Gregory Bunch provides a discussion of Fuzzy Trace Theory (FTT) in an excellent discussion in one of his lectures – The Strategic Leader in a VUCA World. Bunch described the concept of FTT as the role of “verbatim” and “gist” and that they interact like that of an index for a database, where verbatim symbolizes the large amounts of data, words, or numbers; whereas, gist is the one line, the essence, the key idea that summarizes the verbatim. Bunch compares this to something as simple as trying to remember the lyrics of a song, where we can only remember a few lines. However, those few lines are the gist and a simple Google search for those lines or gist now provides us the verbatim or lyrics in their entirety.
Creative Thinking Technique – Lotus Blossom: This is a creative-thinking technique assisting us in expanding our thinking beyond the usual paths of thinking. The authors at InnovationTools.com describe the technique in Articles of Creativity as a creative-thinking technique that will help you expand your thinking beyond your usual paths of thinking – it will help you organize your thinking around significant themes, helping you to explore a number of alternate possibilities and ideas.
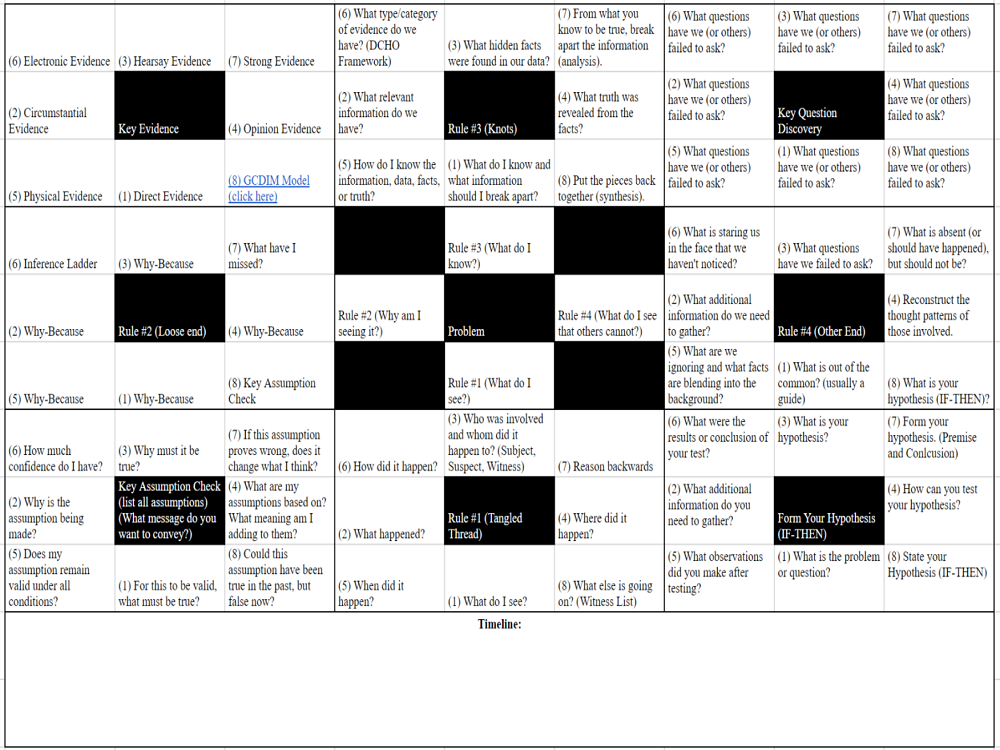
Rule Index = Gist
Let me first explain my idea as a Rule Index using FTT and the idea of the gist as an index for the verbatim. Like the simple rules underlying complexity found in swarm intelligence, Swarm Problem Sensing and Solving possess simple rules assisting us in unpacking a problem.
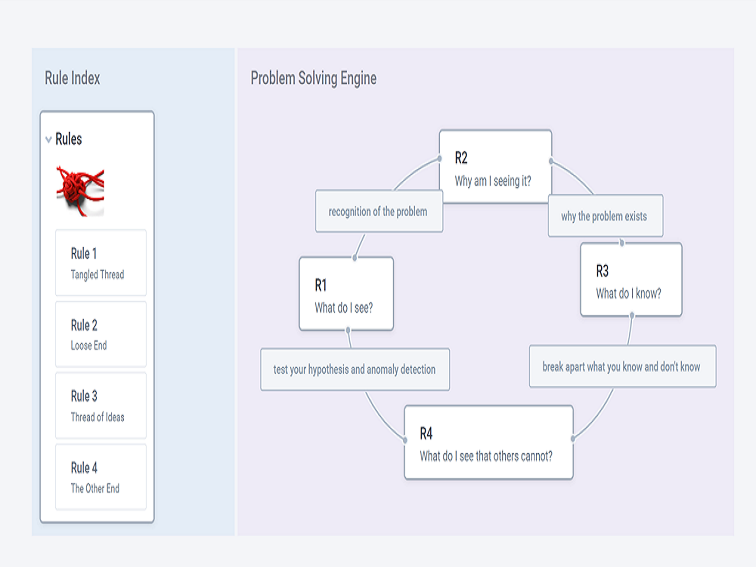
Think of a piece of thread with multiple knots. The first rule is to recognize the problem (the tangled thread). The second rule is to ask yourself why you are seeing the tangled thread (find the loose end). The third rule is to break down each idea (or each knot or thread of ideas). The fourth rule is to find the anomaly or test your hypothesis (find or get to the other end of the thread).
Expanded Version = Verbatim

“Seeing comes from asking really good questions and deeply listening to the context. Questions are asked of the context and about the context. The deeper one wants to inquire, the more aggressive one has to be in terms of opening up the field of questions.”— Ann M. Pendleton-Jullian and John Seely Brown, quoted in Design Unbound: Designing For Emergence In A White Water World
Another way to look at this is to expand the gist getting closer to the verbatim. Let’s look at each rule, along with the following: Purpose, Trigger Question, Metaphor, and Exercise.
Rule #1: Tangled Thread
Purpose: Recognition of the problem
Trigger Question: What do I see?
Metaphor: Physically hold a piece of knotted thread.
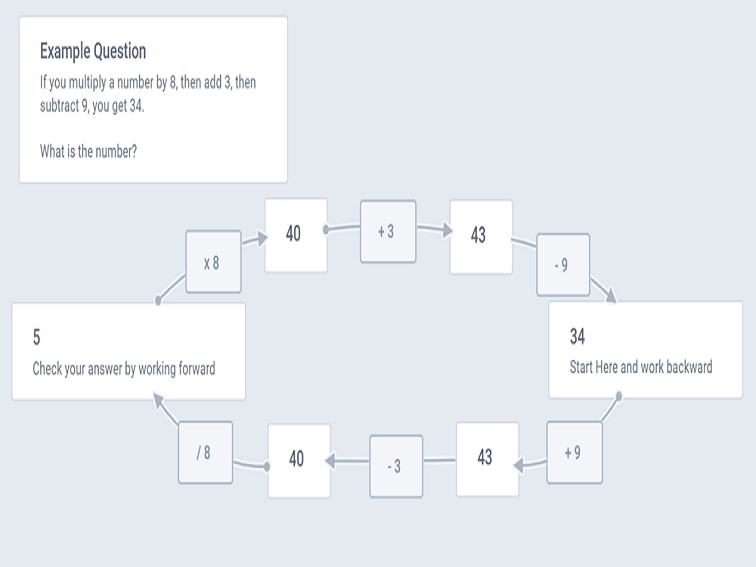
Exercise: Problem-solving by working backward. In Brain Building: Exercising Yourself Smarter, (affiliate link) Marilyn Vos Savant informs us that we should, “Take any problem and work backward from the final sentence in the problem (the one just before the answer) to the final sentence.” A great example of this is the steps in solving a mathematical problem backward.
Step #1: Recognition of the problem. You see a word problem that can be solved easier by working backward.
Example Question: If you multiply a number by 8, then add 3, then subtract 9, you get 34. What is the number?
Step #2: Read and reason backwards. In this example, you are trying to find the number. Start with the last number provided then reason backwards.
Step #3: Check your answers.
Rule #2: Loose End
Purpose: Find out why the problem exists.
Trigger Question: Why am I seeing it?
Metaphor: Find the loose end of the thread.
Exercise: Read the following sentence:
After reading this sentence, you will realize that the the brain does not recognize a second ‘the’.
What if we started by reading a sentence backwards? If we do this, read a sentence backwards (from right to left), we can then find words that might have been missed when reading a sentence from left to right. This helps us get into the habit of reasoning backwards. It forces our linear and logical mind to catch things we wouldn’t normally catch.
Now go back and read the example sentence again, this time read it backwards. Did you notice the second ‘the’?
Rule #3: Thread of Ideas or Knots
Purpose: Break apart information, data, facts, and truth.
Trigger Question: What do I know?
Metaphor: Each knot in the thread is an effect, event, piece of information, piece of evidence (to prove or find the holes), or an allegation to examine. Think of removing the knot or unpacking a problem.
Exercise(s): There are three exercises here to get into the habit of breaking down what you know and what you don’t know.
Exercise #1: The Cartesian Method (aka Hyperbolic doubt or Systematic Doubt). This is an ideal technique for skeptics.
Step #1: Accept only information (facts) you know to be true.
Step #2: Break apart each fact into smaller parts.
Step #3: Order your thoughts by starting with the simplest problem.
Step #4: Rigorously review each thread in the argument.
Exercise #2: Practical approach to the Cartesian Method by breaking down each piece of information or Data Mining.
Marilyn vos Savant, in Brain Building: Exercising Yourself Smarter, discusses data mining using the analogy of panning for gold.
- Information. Break apart each piece of information. First, you scoop up a panful of raw material from a promising riverbed. That’s the information which comes up ceaselessly.
- Data. Select relevant data. Discard most of the information as debris, selecting only those pieces which show signs of being likely to contain gold. They are the data.
- Facts. Find the hidden facts. Hidden in the data are the facts, which contain gold but must be cleansed and refined to remove impurities and reveal its perfections.
- Truth. Reveal the truth or hidden anomalies. Then, and only then, are you rewarded by the gleam of purest gold, the truth.
Exercise #3: In Brain Building: Exercising Yourself Smarter, Savant also provides a great example of approaching mathematics from a new direction by solving arithmetic problems by drawing a picture. This is a simple, yet powerful way to break down a problem or information to see the solution or result clearly.
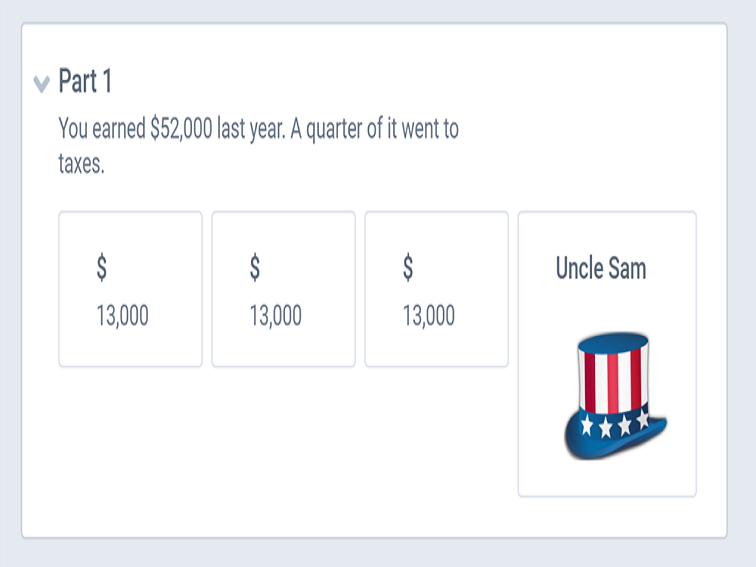
For example, let’s look at the following problem Savant provides us:
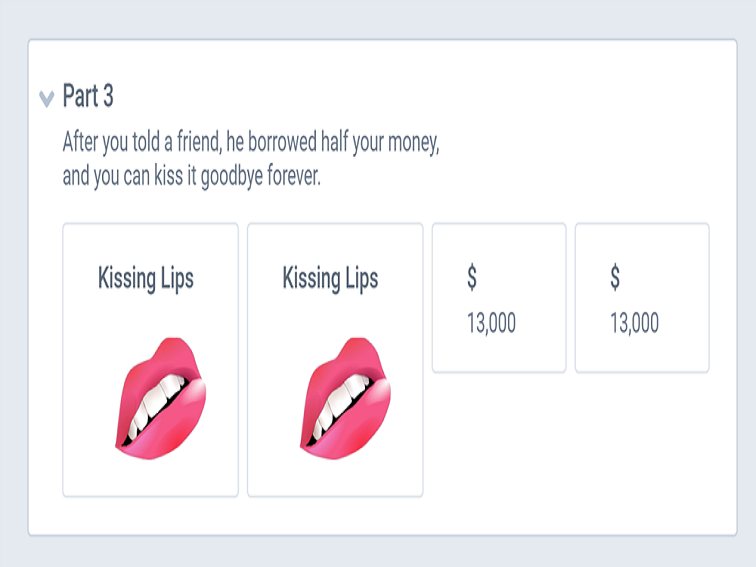
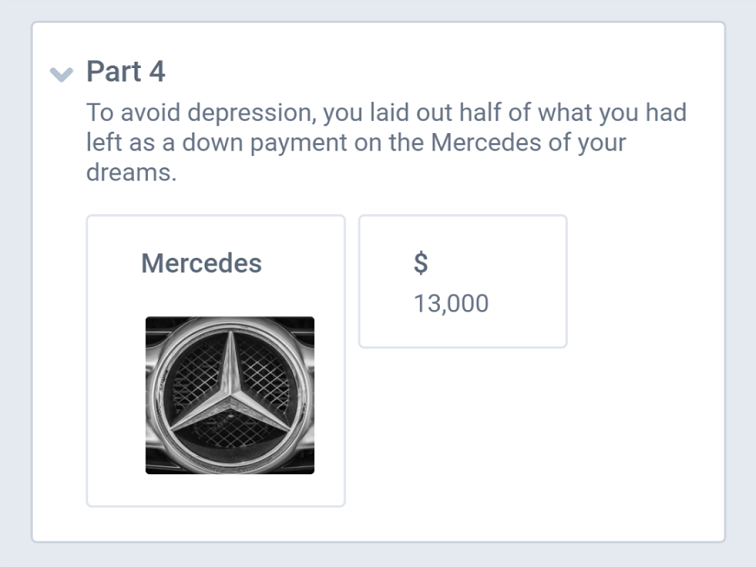
You earned $52,000 last year. One-quarter of it went to taxes. The rest appreciated by a third, thanks to a wildly profitable investment. However, after you told your friends about the stock, one of them talked you into lending him half of your money, and he never paid you back. To avoid sinking into depression, you treated yourself to a down payment on a dark blue Mercedes with half the money you had left.
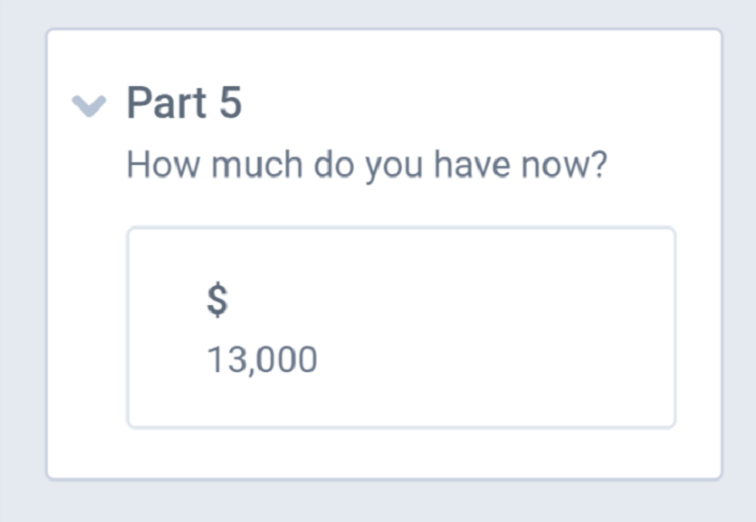
How much do you have now?
To solve this problem, let’s first break the question apart and use drawings or images to solve it (I have recreated the images below).
Part 1
Part 2

Part 3
Part 4
Part 5
Rule #4: The Other End
Purpose: Test your hypothesis and scan for anomalies
Trigger Question: What do I see that others cannot?
Metaphor: Move through each knot to get to the other end.
Exercise: For this exercise, we will unpack the entire Swarm Problem Sensing and Solving metamethod.
Unpacking the Metamethod: Seeing Through Action

Like the Lotus Blossom Creative Thinking Technique described earlier. Let’s now unpack this idea.
Rule Index: Start with the problem then use simple rules as discussed earlier. Let’s examine the index,
Rule #1: Tangled Thread (What do I see?)
Unpack the first rule by answering the questions (refer to the image above). Start with (1) then work in number sequence to (8) similar to the Lotus Blossom Creative Thinking Technique. Continuing with the first rule, break down question (5) by using a timeline.
Rule #2: Loose End (Why am I seeing it?)
We can now move to the second rule. In order to answer the “Why?” we can use the 5-Why technique or Why-Because. Again, start with (1) and work in sequence to (8). To get deeper into the “Why?”, I recommend breaking down step (8) Key Assumption Check, where the goal is to list all assumptions and identify the message that is being conveyed.
Rule #3: Knots (What do I know?)
Continue the same process for the third rule. I recommend using Savant’s Brain Building exercise discussed earlier for this rule. Continue to break down what you know by examining type and category of evidence as identified in (6).
Rule #4: Other End (What do I see that others cannot?)
Think of the fourth rule like detecting anomalies. Here we want to look for those things people typically do not see. Start by looking for things that stand out – or as Sherlock Holmes would say, “What is out of the common is usually a guide rather than a hindrance.” Then start trying to identify those key questions that you should be asking.
Continuing with the fourth rule. You should start to formulate and then test your hypothesis. You will then end with a view from multiple perspectives. Here the goal is to reconstruct the thought patterns of those involved.
Comprehending the Problem
“The act of comprehension means, quite literally, to take hold of something mentally, to grasp it.” – Marilyn vos Savant
You do not have to be a detective, investigator, or expert problem solver to use this method as it is simply a guide to unpacking a problem. A great example of this is (yet again) provided by Marilyn vos Savant in Brain Building: Exercising Yourself Smarter. I highly recommend this book! It’s an older book, but a gem.
Example: The Light Bulb: Turn It On in Your Mind by Marilyn vos Savant
“Take a simple example – a common household light bulb. It’s possible to comprehend how electricity works without going into a study of stationary or moving charges and elementary particles. It is observable in nature – in lightning, in electric eels. We know it is carried across the switch we hit on our wall either releases the current or arrests its flow to the bulb’s filament. When the current is released, the bulb lights up; when it’s arrested, the bulb goes dark. If the filament burns out or breaks, we throw the bulb away and screw in another one. Even without a master’s degree in physics, we comprehend enough about the light bulb so that we don’t have to re-invent it every time we use it.”
My method is like the light bulb example here. It provides a guide to comprehending how the bulb works, yet it does not require a master’s degree in physics.
Lastly, my method will work for both logical and abstract thinkers. It is organized enough for the logical thinkers and abstract enough for the abstract thinkers. In a way, it’s like the Corpus Callosum and acts as a bridge for Right Brain – Left Brain thinkers.