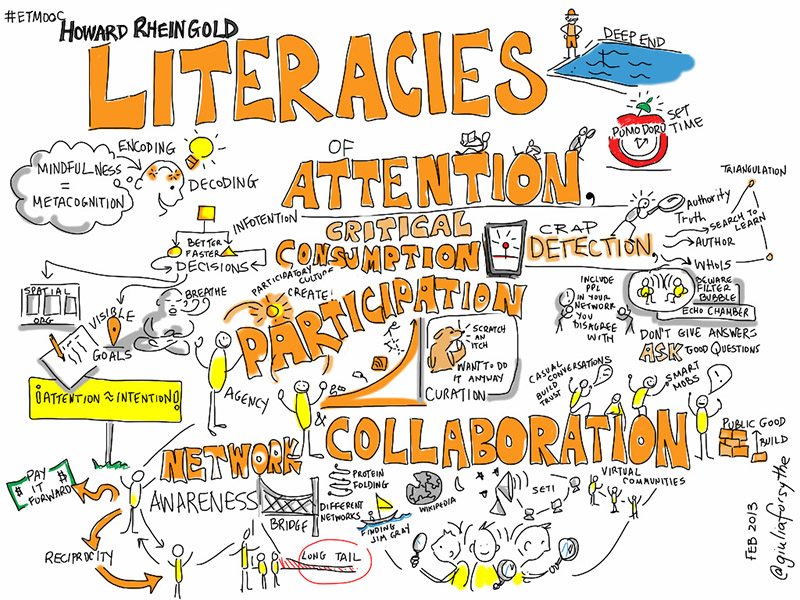
How To Help Students Ask Great Questions
by Terry Heick
Questions can be extraordinary learning tools.
A good question can open minds, shift paradigms, and force the uncomfortable but transformational cognitive dissonance that can help create thinkers. In education, we tend to value a student’s ability to answer our questions. But what might be more important is their ability to ask their own great questions–and more critically, their willingness to do so.
The latter is a topic for another day, but the former is why we’re here. This is part 2 of a short series (can two articles be considered a series?) built around the idea about how to ask great questions as learning tools. Part 1 ‘An Updated Guide For Questioning In The Classroom.’
8 Strategies To Help Students Ask Great Questions
1. TeachThought Learning Taxonomy
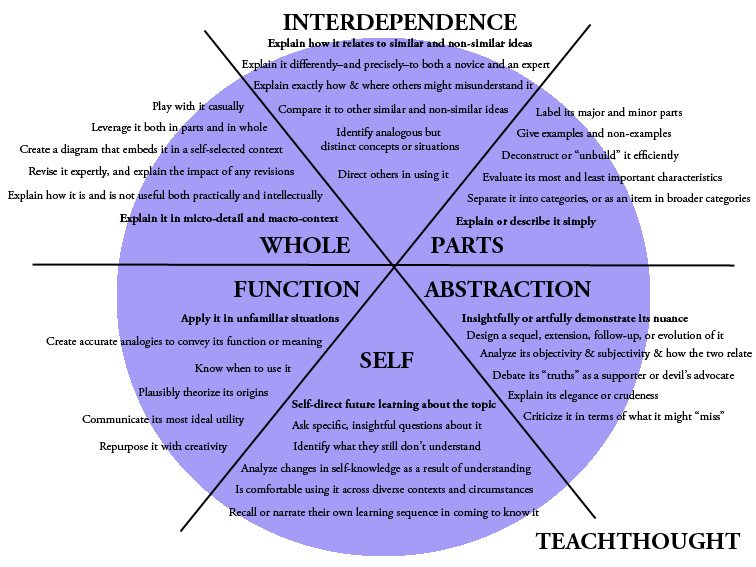
The TeachThought Learning Taxonomy is a template for critical thinking that frames cognition across six categories.
It imagines any learning product, goal, or objective as a ‘thing,’ (i.e.g, a subject of some kind) then suggests different ways to think about said ‘thing’–mitosis, a math formula, an historical figure, a poem, a poet, a computer coding language, a political concept, a literary device, etc. It’s designed to promote ‘whole’ thinking about otherwise discrete or disconnected ideas.
1. Function–thinking critically about how a ‘thing’ works
2. Self–Making sense of how the thinker relates to the ‘thing’
3. Abstraction–Thinking about the ‘thing’ creatively, or in non-traditional ways
4. Parts–Seeing the individual parts of the ‘thing’
5. Interdependence–Examining how the ‘thing’ relates to other (similar and non-similar) things
6. Whole–See the ‘thing’ fully and within context
A literary device–a metaphor example, is usually studied in isolation. This writer uses this metaphor in this way to this effect. Using the TeachThought Learning Taxonomy, a learner would be forced to confront that metaphor in much more diverse cognitive terrain–to think about something in multiple ways for a more complete picture and advanced understanding.
Function–Communicate the metaphor’s most ideal utility (how it can and should be used, and why).
Self--Identity what you do and don’t understand about the metaphor
Abstraction–Design a ‘sequel’ of the metaphor (not a simile–an extended metaphor would be a good start)
This framework can be used not only as a planning or assessment tool, but to promote students in self-directed learning and self-created questioning and examination. In short, they can use this framework (or a simplified version of it) to create their own questions. Some examples?
Prompt: Parts–Give examples and non-examples
Questions: What are 3 examples and non-examples of mammals? What are 5 examples of push-pull factors? What are 3 non-examples of mixed fractions?
Prompt: Interdependence–Direct others in using it
Questions: How do–or might–others use alternative fuel sources to help create fresh water sources?
Prompt: Explain it differently to a novice or an expert
Questions: How would explain the Pythagorean Theorem differently to a 2nd grader and a college freshman? What would the main difference be?
The downside to using the TeachThought Learning Taxonomy to help students ask their own questions is the relative complexity of the framework, and the extra step of converting prompts to questions. Therefore, it’s better suited to late middle school–university settings.
The upside? It can be used in any content area to think deeply about almost anything.
2. Digital Taxonomy Power Verbs
‘Power verbs’ aren’t exclusive to Bloom’s Taxonomy (see below). In addition to our TeachThought Learning Taxonomy (see above), there are ‘verbs’ that describe cognitive ‘actions.’ Add some kind of framework or hierarchy, and you’ve got a full ‘taxonomy.’
Enter the ‘digital taxonomy’ power verbs. You can download a ready-for-the-classroom curricula version of our power verbs here, but you can do plenty with digital taxonomy power verbs to help students ask great questions without spending a penny. From designing projects and refining assessments to classroom, discussions and digital citizenship lessons, the ‘actions’of students are among the most critical components of any learning experience.
3. Socratic Discussion
A Socratic Discussion, which is also referred to as a Socratic Seminar, is a group learning strategy designed to support students in open-ended examination and extended critical thinking through dialogic terms. In short, students learn together by talking together in an open and student-centered format. These discussions are not teacher-led, but student-led–students talk to one another.
It is a dialectal method of learning inspired by Socrates’ iconic teaching methods that depend on a pattern of theory formation, revision, and elimination to arrive at loosely-held “truths.” Used strategically, this approach should promote inquiry as learning and the close examination of one’s own beliefs as primary catalysts for learning.
4. Paideia Seminar
A Paideia Seminar is similar to the Socratic Seminar–in fact, it uses Socratic Discussions on the part of the students, combined with a minor but clear role for teachers, to facilitate verbal and critical examination of ideas. From the (a?) Paideia Seminar website, “The Paideia Seminar is an integrated literacy event built around formal whole-class dialogue. The purpose for doing Paideia Seminar is to support students’ ability to think conceptually and communicate collaboratively.”
One of the key differences between a Paideia Seminar and a Socratic Seminar is that within the Paideia format, teachers are “allowed” a role, provided that that role doesn’t exceed 10% of the total discussion. You can see a video here to learn more.
5. The Question Game
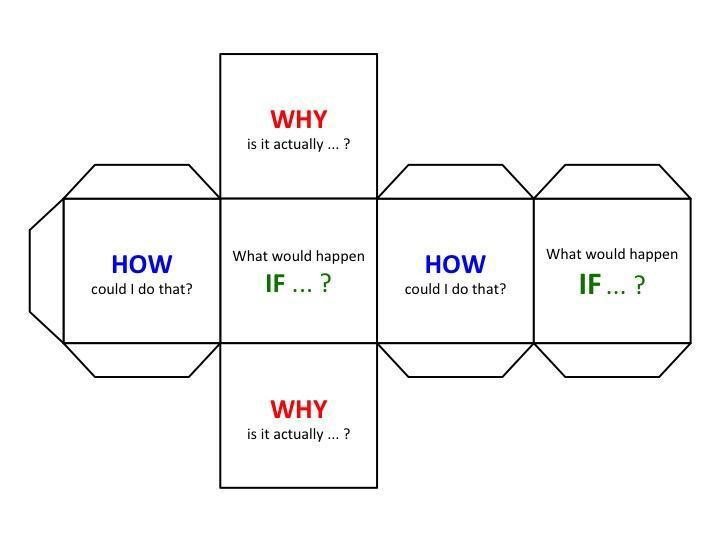
The Question Game focuses on “teaching children a kind of thinking which is particularly useful in creative problem-solving–a focused approach to get from a problem to the most effective solution. It is most effective when combined with regular repetition, which solidifies the thought pattern, and with groups, which encourages contributory exploration of alternative responses and creativity.”
Its dice-form not only offers a whiz-bang manipulative, but also introduces a level of gamification and playful uncertainty into the process, and its open-ended and universal stems make it practical for a wide variety of classroom applications.
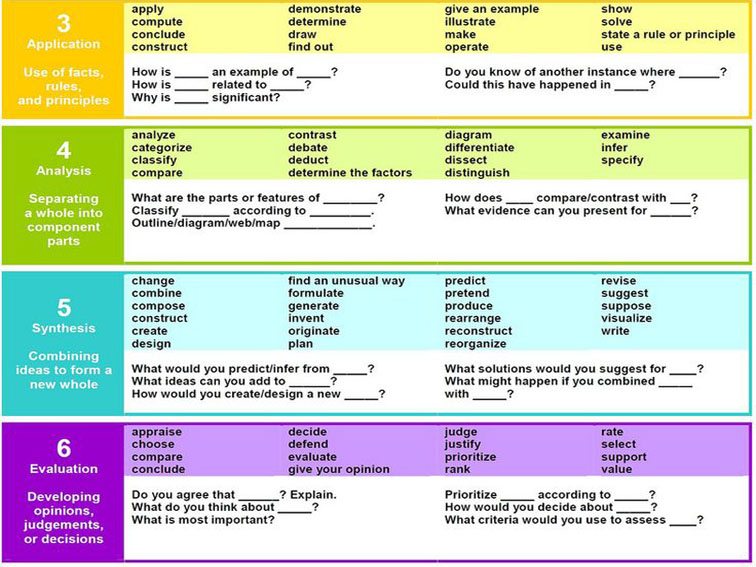
6. Bloom’s Taxonomy
Similar to the TeachThought Taxonomy, Bloom’s Taxonomy can act as a framework or pattern to funnel content, inquiry, or other learning processes. These use of the taxonomy to create universal stems is one approach as modeled in the following graphic from flickr user enokson.
7. Question Formulation Technique
We’ll have more on this soon but in short, the Question Formulation Technique (QFT) is a kind of question brainstorming process based around a topic as a kind of kernel.
In their words of the Right Question Institute, QFT is “straightforward, rigorous process that helps all students learn how to produce their own questions, improve their questions, and strategize on how to use their questions. In the process, they develop divergent, convergent and metacognitive thinking abilities.”

For now, you can read more about the QFT here.
8. Question Stems
As seen in the Bloom’s graphic, sentence stems and question stems are wonderful tools that can empower students to ask questions by giving them a head-start in doing so.
By using a ‘stem,’ a teacher has set the ball on the proverbial tee for the student to smash. Yes, ideally the student asks their own great questions, but what if they can’t–or don’t think they can? What if they don’t? What if they’re still learning how? What if they lack the background knowledge in some narrow sect of science or math or whatever, and need a push in the back? Stems can help.
See also 26 Sentence Stems For Higher-Level Conversation In The Classroom
Question stems are a more elementary questioning strategy than the Question Formation Technique (see above), but not necessarily less effective. They can be used for younger students, students struggling with a concept, or even “advanced learners” (not a huge fan of this term) as they narrow an open-ended learning experience, or to be used as ‘bread crumbs’ in the case that the teacher is trying to help them arrive at a pre-determined destination. Some examples?
8 Basic Question Stem Examples
Which differences between ____ and ____ stand out to you?
Why does____never seem to____?
How does_____impact____?
How does _____ work?
What’s most important about?
What’s most simple/complex about ______?
How could you classify____? (And ‘Why would you classify____?’)
When____, why does____?
8 Strategies To Help Students Ask Great Questions; image attribution flickr user enokson